- --> 非磁性金属(Fermi液体、Luttinger液体...)
- --> 反強磁性Heisenberg模型(VB,スピンの量子効果...)
どうひねくっても、強い磁性は出てこない
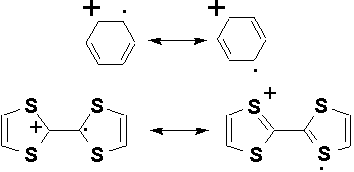
π電子系にホールを1個ドープした系の模型

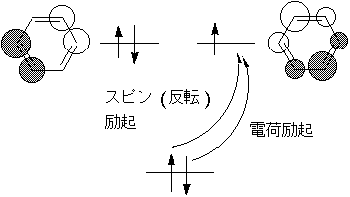
(ベンゼンを例にしたので軌道縮重がありますが、無視してください)
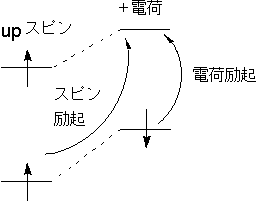
↑軌道と↓軌道の形も異なってくる
スピン分極の原因=分子内Coulomb反発(Exchange)
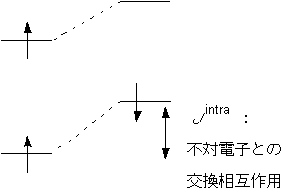
別のいい方: 不対電子による“磁場”で
一重項VB(下の軌道)が緩められた
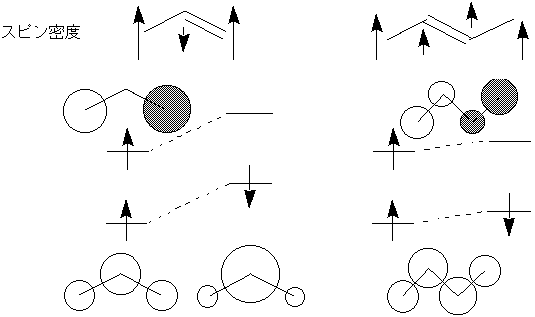
トポロジー的なスピン分極制御=分子磁性の常套手段
- 分子自身のスピンを大きく(高スピン分子)
- 分子間でスピンを揃える(--> 強磁性etc.)
Dynamic spin polarization(今ホットなテーマ)
=電荷自由度とスピン自由度
ラジカルのイオン化によってスピンはどうなる?
スピン分極を使った分子間強磁性相互作用
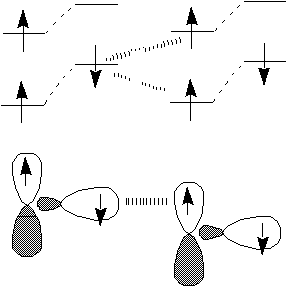
- 量子スピンフェリ磁性と見ることも可能
Bipartiteで副格子サイト数の異なるhalf-filled Hubbard模型は、
Lieb定理から必ずフェリに- VBSをRVB的にした、ともいえる
再びトポロジー的条件:
分子間SOMO-SOMO でなくて、
分子間SOMO-HOMO, HOMO-HOMOが有利
このモデルを強相関Hubbardモデルに焼き直すと、
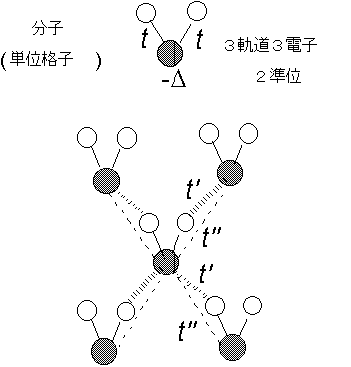
実はこれは、
- 有機強磁性体β-p-NPNN
- 田崎らによる平坦バンドHubbard強磁性
- Mielkeのカゴメ格子平坦バンドHubbard強磁性
と同じトポロジーをもっている
次のモデルで、
1/6-filled(3つのうち一番下のバンドがhalf-filled)のとき、
基底状態は安定な強磁性である (Mielke and Tasaki, 1993)
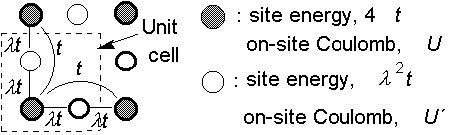
一電子Hamiltonian
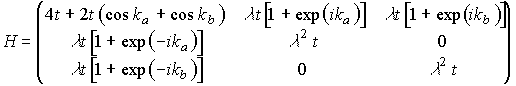
バンド計算から、
最初の2つは平坦バンド
--- なぜ平坦か・・・ 非 結 合 性 だから
有効スピンHamiltonianで、
J ∝ 連結サイトのon-site U
制限を緩める理論が発展中(half-filledからのズレ、弱い分散)
==> 金属強磁性へ
トポロジー条件: VBが描けないところに
スピンが余る(強相関的表現)
弱相関でもOK(バンド計算でわかる)
結局、分子磁性のスピン整列規則とほとんど等価
共 通 点 :
- トポロジーの支配,
- Hund則と縮重
新たにわかったこと:
- バンド計算との関係
- 厳密な意味での “connectivity”
- 非結合性をもたらす第2近接 t
孤立平坦バンド模型は、伝導性にとってはやや非現実的
複数軌道強相関系としては
むしろ、近藤格子(例:π-d 相互作用系)がありえそう
近藤格子のVB描像 Periodic Anderson Hamiltonian
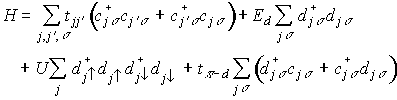
- 第1項:πバンド
- 第2項:d 準位
- 第3項:d 軌道のon-site Coulomb
- 第4項:π-d 混成
--> 摂動でs-d Hamiltonian
J=−8t 2/U
一種のt -J model
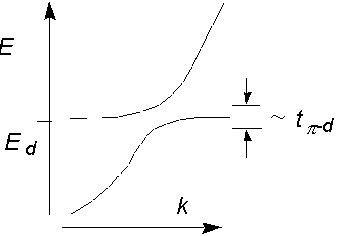
- VBS:VB電子対は静止
- RVB:VB電子対は動く
- 近藤格子:VB電子対の一方は静止、他方は動く
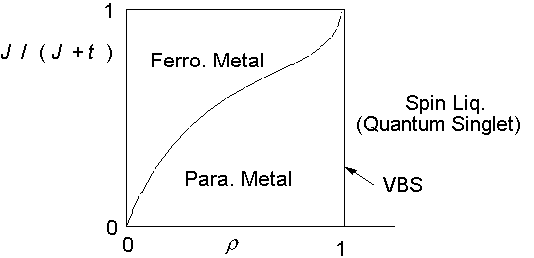
二重交換相互作用系=近藤格子でJ>0(Hund)の場合
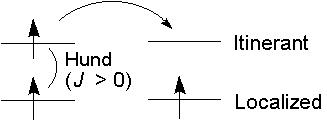
こちらは、実際に室温で金属強磁性・巨大磁気抵抗
が出ている(Mn perovskite)
強磁性(あるいは磁気秩序)は、いったんできてしまえば、
スピンの量子性という観点からは陳腐にみえるが、スピンを揃えるというこ
とに、量子力学の本質(位相の問題・電子相関など)が深〜く関わっている
のである。
| Tamura's Home Page | 目次 | [1] | [2] | [3] | 参考文献 |
|---|---|---|---|---|---|
| (4−1) | (4−2) | (4−3) | (4−4) |
〒274 船橋市三山2-2-1 東邦大学 理学部 物理学科
Phone : 0474-72-6988, F A X : 0474-75-1855
田村 雅史
tamura@ph.sci.toho-u.ac.jp