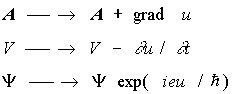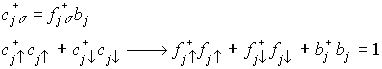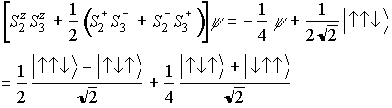[2]低次元磁性
(2−1) Spin-1/2 Heisenberg 一次元鎖
・・・ J J´
J J´・・・
- J,J´>0(強磁性的)
- 基底状態は強磁性(ただし一次元最近接系なのでTC=0)
- VBなし
- χは低温に向かって単調増大
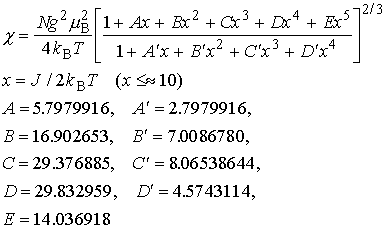
- G. A. Baker et al.: Phys. Rev. A
135 (1964) 1272.
- Y. Nakazawa et al.: Phys. Rev. B 46
(1992) 8906. の中の
- γ-p-NPNNの解析と文献も参照
- J < 0 <J´( J´--> ∞ で
Haldane 系)
J <J´< 0(Alternating antiferromagnetic
Heisenberg chain=AAHC)
- J=J´<0(Uniform Heisenberg
Chain)・・・特異点
いわゆるBonner-Fisher
- 基底状態はスピンが縮んだNeel(反強磁性TN=0)
- VBの入り方は2通り(非直交)が縮退(uniqueでない)
- 1つに決めると並進対称性が破れる
- スピン液体というそうです(Cf. RVB)
- ギャップなし、スピン波近似OK
- スピン相関は距離のベキで減衰
- χは丸いピークを持って、T-->0でχ>0(gapless)
- T=0で、M
はH=0からlinearに立ち上がる(gapless)
- Bethe-Hulthenによる厳密解がある
- 基底エネルギー: E=[1+2 (2 ln 2-1)] NJ / 2
- 励起エネルギー:ΔE=−Jπ|sinq |
(スピン波)
- 磁化率の数値fitting
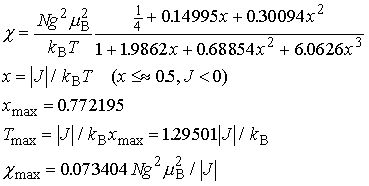

- W.E. Hatfield et al.: Inorg. Chem.
19 (1980) 3825.
- ( x の定義が分母分子逆)
- 極大値の計算は筆者
(2−2)Haldane系とVBS(Valence Bond Solid)
Haldane's conjecture
「一次元Heisenbergスピン鎖の基底状態は、
- S=1/2, 3/2, ... (半奇数)のときgapless、
- S=0, 1, 2...(整数)のとき、縮退なしでgapの下」
(S=0の場合は自明)
なにゆえstrikingだったか?
「 古典的な理論からすると、Sが整数か否かで
系の基底状態の性質が定性的に異なるのが信じ難い」
S=半奇数のとき、スピン波理論がよい近似
- 励起状態は、基底状態のスピンを少しずつねじったもの
- 一次元の場合、反強磁性スピン相関が距離のベキ関数
S=整数のとき、スピン波理論は破綻
- 基底状態のスピンをねじった状態が基底状態と非直交
- あとでわかることだが、結合電子対の片方の電子の
スピンを少しねじった状態が意味をなさないのと同様
Haldane基底状態の理解(厳密証明はまだ)
次のVBS(Valence bond solid)状態がよい近似
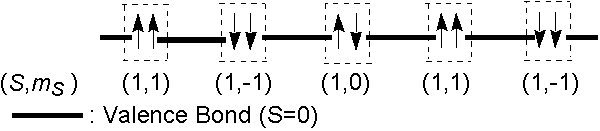
(S,mS
)は、VB両端がS=0になるように
量子的に揺らいでいる(ゼロ点振動)・・・下図

- 三重項の内部揺らぎとVBの一重項反対称性がマッチ
- ミソは、S=1が2電子からできていること
- 次のHamiltonianはVBSが厳密な基底状態
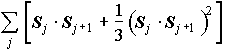
基底状態の別の表現(隠れた秩序)
「mS=1と−1が交互に並んだ状態に
適当にmS=0を挟んだもの
(これを称して乱れているという)」
ちょっと考えればわかるが、mSの配列として、
1,1とか1,0,1とか-1,-1とか-1,0,0,-1は、
VBS配列を破壊している
(これもスピン液体というそうです)
スピン相関
- 距離の指数関数で非常に速く減少
---- 一般に、化学結合系の結合力はかなり局所的
- mS=1と−1の間にmS=0をいくつ挟んでもよいことに対応
VBS基底状態からの励起
- スピンを少しずつねじったスピン波状態ではない
(そもそもねじるべきスピンが消失している)
- VBを1つ切断した状態(の線形結合)〜三重項
- VBの切断= local には一重項-三重項のCrossover
- VBの切断エネルギー〜結合エネルギー 〜 Haldane gap
有限Haldane鎖の特徴(疑似四重縮重)
反強磁性スピン相関は短距離で減衰
--> 両端のVBSに参加しないスピンはほとんど無相関
両端の2スピンについて、
S=1(三重縮重)とS=0とがほとんど縮重
 要するに、ほとんど常磁性
要するに、ほとんど常磁性
(2−3)Haldane系の仲間
- 一次元系
- J<0<J´( J´--> ∞ で
Haldane系) と
J<J´<0(Alternating antiferromag. Heis.
chain)
- いずれも非磁性一重項基底状態の上に gap
- J<J´<
∞で、相転移はない(J´がferroだろうとantiferroだろうと...)
- 熱力学的には同じ性質
- 励起状態の波数依存性が異なる(励起三重項をつくる場所の問題)
- VBSが一意的につくれる系
- 有限系
- 端がない系=非磁性分子
- 端がある系 -->
疑似四重縮重を示す系(量子効果の効き具合)
- 二次元以上
- 一意的なVBSの構成可能性(トポロジー条件):
「
スピン量子数の2倍2Sが、最近接数の整数倍かどうか?」
例)S=3/2の蜂の巣格子(グラファイト型),S=2の正方格子,
ダイアモンド格子、etc.
(ポリエチレンもダイアモンドも原子間距離が長ければ...)
- だが、高次元になるとスピン相関が伸びる -->
磁気秩序の可能性
- Spin Ladder(偶数本鎖)
補足: Spin ladderの磁性(基底状態)
- leg (梯子の長手方向) :J
- rung(梯子の踏むところ):J´
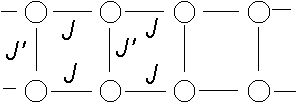
- J, J´>0・・・基底状態は強磁性(自明)
- J, J´<0
- 偶数本(2-leg ladder etc.):spin gap あり
- 奇数本(3-leg ladder etc.):spin gap なし
- J´<0<J
- leg1本は古典スピン的 --> Neel反強磁性?
- S=0 の一次元鎖 -----> 非磁性 with spin
gap?
- Heisenbergスピンでは実際には後者(非磁性)
- Ising的にするとNeel, XY的にするとKT
- J<0<J´
- Haldaneからの類推:
- 偶数本(2-leg ladder etc.):spin gap あり
- 奇数本(3-leg ladder etc.):spin gap なし
- ところが、VBSの作り方は一意的でない
(RVBかVBSか直観的には判断に困る)
(が、たぶん、どちらも並進対称性を破らないので)
- Heisenbergスピンでは、偶数本で Haldane-like な非磁性
- 強くIsing的にするとNeel,
- XY的にするとKTを経てFerroへ
結局、偶数本鎖の Heisenberg spin ladderは、
J,
J´>0以外では、非磁性量子一重項基底状態
(2−4)二次元系
二次元Heisenberg強磁性体
- T=0まで長距離秩序なし(Mermin-Wagnerの厳密証明)
- KT(Kosteritz-Thouless)転移(特にXY model)
- ある温度以下で磁化率発散
- その温度以下:スピンの渦が対をつくる
=渦はエネルギーが高いので少ない
- その温度以上:スピンの渦は無制限にできる
- 超伝導のvortex状態に対応
二次元Heisenberg反強磁性体(S=1/2)(高温超伝導の母体)
- 基底状態の証明はない
- T=0まで長距離秩序なし、gapなし、と信じられている
- 一次元uniform chainとよく似ている
(2−5)三次元
- 弱い鎖間/層間相互作用の役割(現実の物質)
- 短距離秩序(short range order) --> 長距離秩序
- 短距離秩序で鎖・層のSが大きくなったら古典化
- とりあえず、平均場で扱える
- こういうとき、メタ磁性が起こりやすい
- メタ磁性=「反強磁性-->磁場誘起強磁性」の転移を示すもの
- 鎖内/層内が強磁性で、鎖間/層間の弱い反強磁性的
- 相互作用のせいで全体が反強磁性になっているとき
- 外部磁場のZeemanエネルギーが
- 反強磁性的相互作用に勝てば、強磁性になる
- Spin Flop との違い
- Spin flopでは、一次相転移でスピンがまだ磁場に対して
傾いた状態になる
- メタ磁性では、一次相転移でスピンがいきなり磁場方向に
向いた状態になる
- 本物の三次元: flustrationがなければ、たいてい秩序化する
- 立方格子S=1/2 反強磁性Heisenberg modelは証明あり
(2−6)Flustration(低次元に限った話ではないが)
- 典型例: Ising三角格子(基底状態は∞重縮重)
- T=0でエントロピーが
non-zero(熱力学第三法則の対象外)
- 古典Heisenberg三角格子
- 120度構造の秩序
量子スピンの立場から注意
少なくとも有限系では
- 3N個の 整数スピンから
S=0(縮重なし)が作れる
(Andersonが昔、三角格子でRVBを...)
- 3N個の半奇数スピンからS=1/2(2重縮重)が作れる
低次元系のまとめ
- 揺らぎが大きい(なかなか磁気秩序を示さない)
- 量子効果が強い(最近接数が少ない)
- 非磁性基底状態になるか否かはVBのトポロジーで決まる
- 反強磁性がnon-uniformに入ると、VBSができて
ゼロ次元に持っていかれる(かえって次元性を下げる)
([2]の終わり)
[3]強相関系の磁性
(3−1)Hubbard modelとHeisenberg model
3-1-1. 2-site Hubbard model(水素分子の模型)
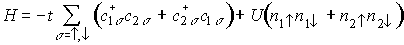
- t : transfer積分(Huckelの共鳴積分と同内容)
- U: on-site Coulomb反発
演算子の公式(c+,
c:fermion演算子)
- c+|0>=±|1>
- c+|1>=0
- c |0>=0
- c |1>=±|0>
複号: 左に電子が偶数個なら+、奇数個なら−
反交換関係:
- c+j
c+k=−c+k
c+j,
- c j c k =−c k
c j
- c j c+k
=δj k−
c+k c j
n: 数演算子
nk=
c+k ck
行列要素の計算
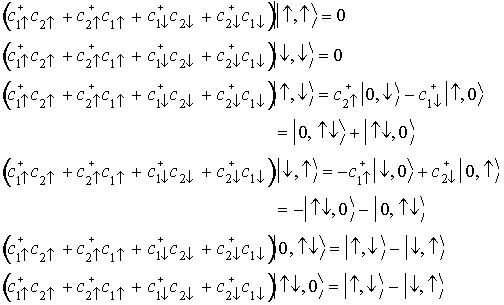
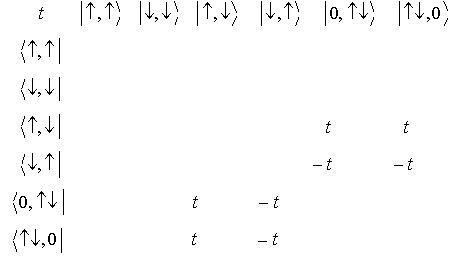
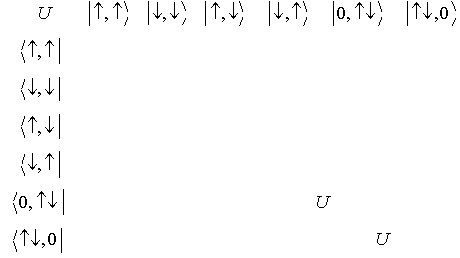
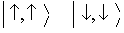 はそのままE=0の固有状態
はそのままE=0の固有状態
残りの 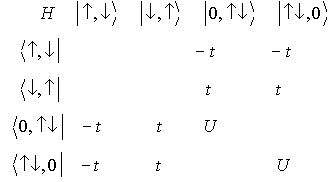 の対角化
の対角化
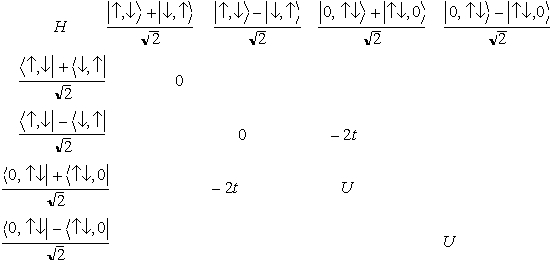
==> 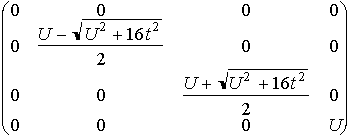
- 基底状態(一重項・結合性):
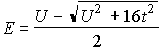
- 三重項状態(非結合性)
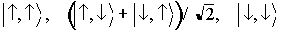
:E=0
- イオン化状態(一重項) :E=U
- 反結合性的状態(一重項) :
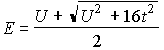
基底一重項 --> 三重項への励起エネルギー
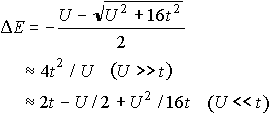
これを交換相互作用と見なして、2J
と書く(kinetic exchange)
( t なしでも出てくるものはpotential
exchangeという)
===> 低エネルギー部分は、Heisenberg model に帰着
U が大きくなると、基底一重項が不安定化
一般に、電子相関が強くなると、
イオン化配置が不安定化(電荷自由度減少)
--> 基底一重項の安定化への寄与減少
--> 磁性(スピン自由度)が出やすくなる
電荷揺らぎ(自由度) vs.
スピン揺らぎ(自由度)・・・互いに拮抗
3-1-2. t -J model
以下、強相関(U >> t )とする
基底状態付近・・・2J=4t2/U のHeisenberg
modelで記述
(スピン自由度のみ考慮)
一般に、U >> t のHubbard model
(1/2-filled)は、
2J=4t2/U の Heisenberg
model に帰着
ホールの占有数を制限: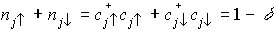
次の変換で、スピン演算子をつくる
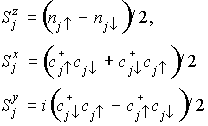
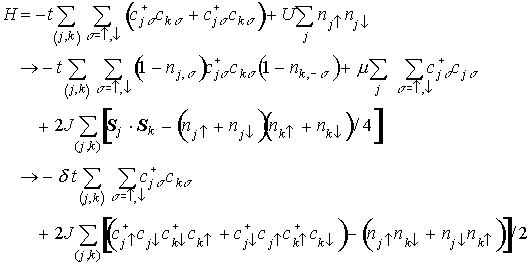 (t-J model)
(t-J model)
- 第1項: 電荷自由度
- 第2項: スピン自由度
- δ:占有数制限(half-filledでδ=0)
さらに、
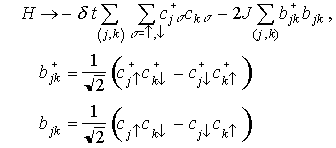
- 第2項: VBのエネルギー(見かけ上はVBの一体問題)
- (b+, b :singlet
VBの生成・消滅演算子)
これも t-J
model(スピン自由度はVBの形成・切断で表現)
3-1-3. 寄り道:VBのもつ対称性
局所gauge不変性: 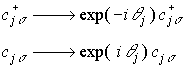 で b+, b不変
----->
局所量子位相θjの任意性=局所粒子数保存
で b+, b不変
----->
局所量子位相θjの任意性=局所粒子数保存
“ベクトルポテンシャル”(磁気;運動量)と
“スカラーポテンシャル”(電気;座標)の任意性
Gauge変換
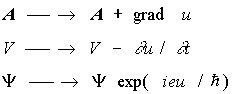
- 粒子の遍歴 --> 位相を揃える
- 粒子の局在 --> 数を保つ
・・・ 化学結合(b+,
b)の物理的本性でもある
HamiltonianのTransfer項も局所gauge不変となるには、
t jk --> t jk
exp[ i(θk−θi )]
ベクトルポテンシャルAがあれば、t
jk はt jk exp[ iea A
ki ]
局所gauge不変条件から、
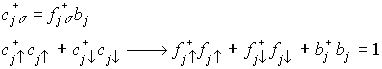
つまり電子を、
- up-spinとdown spin、電荷0のfermion f
- spinなし、電荷+1 のboson (ホール)b
に分解
分解したまま( f と b
が別々に励起できる)なら、
スピン-電荷分離(Luttinger liquidなど)
スピン-電荷分離と分子の問題については後述
(3−2) 有限Hubbard模型
・・・
Lieb定理、
あるいは Longuet-Higgins予想
Lieb-Mattis定理
- Lieb定理 (half-filled Hubbard model)
- Lieb-Mattis定理 (量子反強磁性Heisenberg model)
- Longuet-Higgins予想(Huckel交互炭化水素)
前提:
bipartiteな格子で、最近接相互作用のみ考える
bipartite とは
A,B2つの副格子に分割できて、
Aの最近接は全部B、
かつ、Bの最近接は全部A
=“交互炭化水素”・・・オルト-パラとか...(偶数員環)
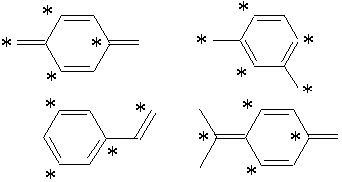
S=|*付原子数−*なし原子数|/2
基底状態のSはそれぞれいくつ?
(トポロジカル条件)
定理の主張
- 副格子AとBが同じサイト数(有限)なら、基底状態は1つでS=0
- サイト数が異なれば、基底状態で、
S=[非結合性軌道(電子)の数]/2=|サイト数の差|/2
後述の分子磁性のトポロジカル規則の基礎
無限系への外挿(要注意!簡単な話ではない!)
S=0基底状態がそのまま無限系の
非磁性状態になるとは限らない
エネルギーギャップが有限にとどまるか?
- 有限 --> 非磁性基底状態
- ゼロ --> 対称性が破れるか?
- 破れない --> 常磁性(例えば Bonner-Fisher)
- 破れる -->
磁気秩序(Neel反強磁性,複数基底状態)
例えば、
偶数員環のような圧倒的安定一重項になるか、
両端のあるHaldane系のような
ほとんど常磁性に近い一重項になるか、
は、議論を先に進めないとわからない。
(3−3) RVB
反例:gap がゼロに向かう場合(Bonner-Fisher)
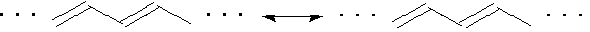
共鳴のメカニズム
1)スピンの量子性(交換量子トンネル)
1−2−3系で、1-2間 mS=1/2
VB状態
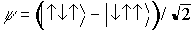
にS2・S3を作用させると、
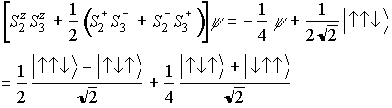
つまり、1-2間VBが壊されて、
2-3間VBができる (VBが動いた)
*注意: 電荷自由度なしでもRVBはあり得る
2)電子の遍歴性(half-filledでない場合)
ホールとVBが互いに動く(分離もする)
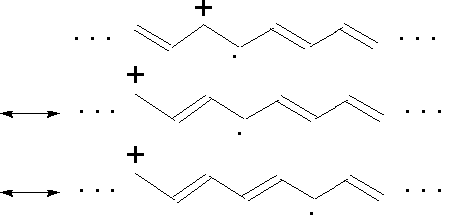
- 高温超伝導で有名になったもの
- 結合交代なしのポリアセチレンやK-TCNQも
- 反強磁性相関に関係するspin (pseudo)gap?
--> VBの切断エネルギー〜J(とすればspin gap)
--> 超伝導機構に関係がある?とかないとか...
J と t
は、VBを動かすという点では似ているという話
だが、1)と2)ではかなり性質が違うそうである
([3]の終わり)
〒274 船橋市三山2-2-1 東邦大学 理学部 物理学科
Phone : 0474-72-6988, F A X : 0474-75-1855
田村 雅史
tamura@ph.sci.toho-u.ac.jp
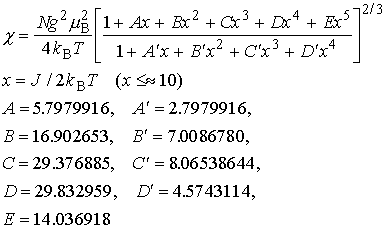

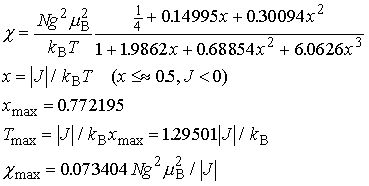

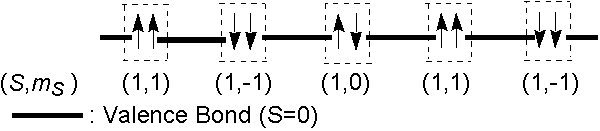

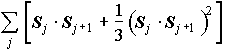


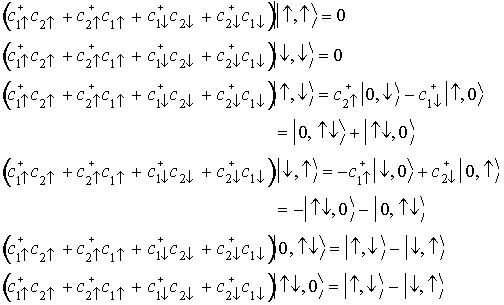
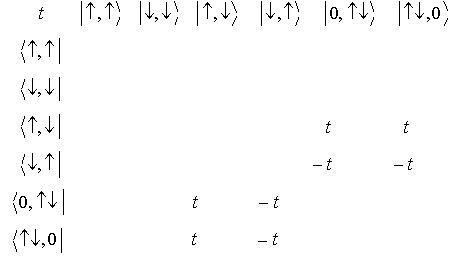
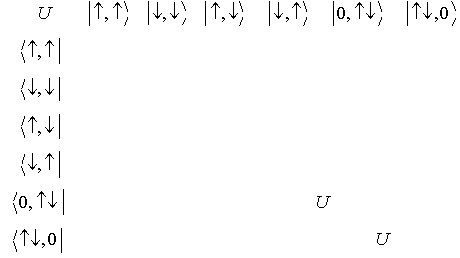
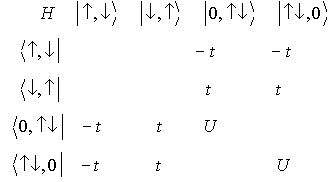 の対角化
の対角化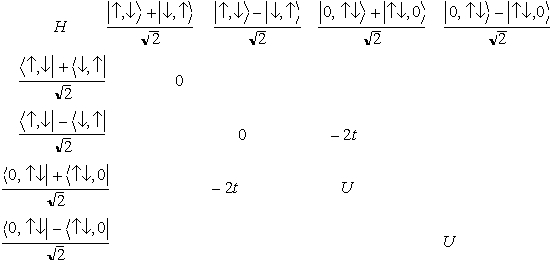
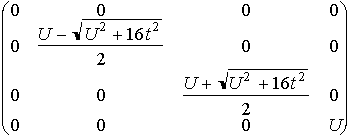
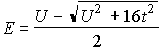
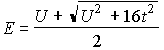
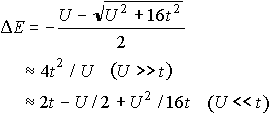
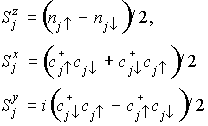
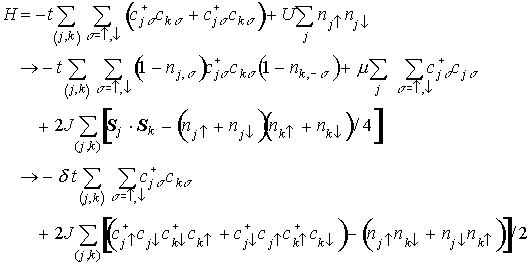
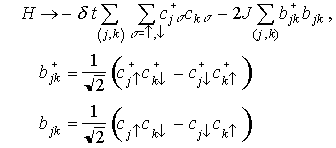
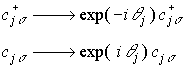 で b+, b不変
で b+, b不変