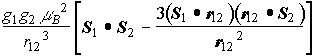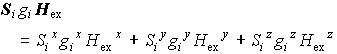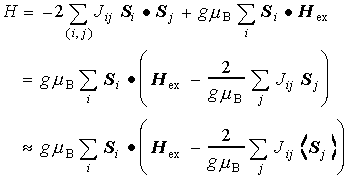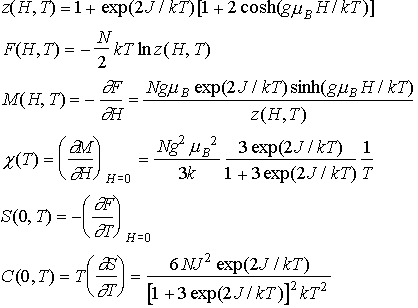[1]量子スピン系入門
(1−1)量子スピンの基本
1-1-1. Heisenberg spin Hamiltonian
:スピンの自由度だけ
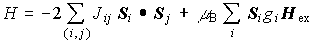
交換相互作用とZeemanエネルギー
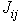 :交換相互作用 exchange coupling
:交換相互作用 exchange coupling
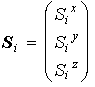 演算子を成分とするベクトル
演算子を成分とするベクトル
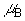 :Bohr磁子magneton
:Bohr磁子magneton
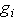 :g テンソル(3×3行列)
:g テンソル(3×3行列)
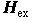 :外部磁場
:外部磁場
- 電子の磁気モーメント:μ=−gμBS
1-1-2. 電子1個
・・・ S=1/2(spin-1/2);
mS=−1/2, +1/2 (上向き, 下向き)
(一般にmS=−S,−S
+1,...、S−1,S
の2S+1通り:スピン多重度)
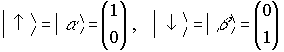
2つの状態=二重項(doublet)
スピンの量子揺らぎ(ゼロ点振動)
- 量子スピンのベクトルはまっすぐNやSを向かない
- 歳差運動 Szを確定させると、SxとSyは不確定
演算子の公式
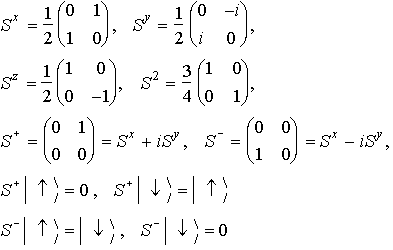
1-1-3. Heisenberg交換相互作用
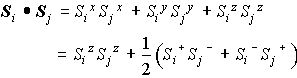
- 対角項(古典的;Ising)と非対角項(量子的共鳴を起こす)
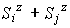 は変えない−−>
は変えない−−> 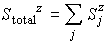 は変えない
は変えない
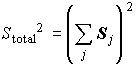 も変えない
も変えない
- 交換関係:
1-1-4. 2電子問題(最も簡単でもっとも重要な例題)
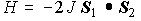
一般に、2N通りのスピン配置(N:電子数)・・・今は4通り
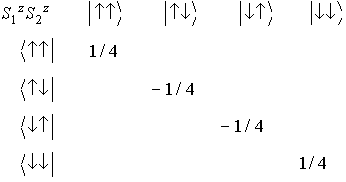
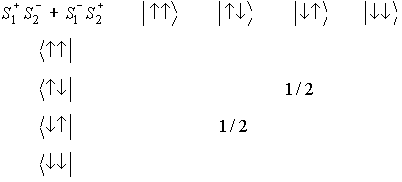
H を対角化して、
E=−J/2; |↑↑>,|↓↓>,
(|↑↓>+|↓↑>)/√2
E= 3J/2; (|↑↓>−|↓↑>)/√2
古典 −−−−−−−>
量子
強磁性(平行) 三重項(S=1)
反強磁性(反平行;Neel) 一重項(S=0;非磁性VB)
2電子系基底状態の性質
J>0(Ferromagnetic)・・・・古典も量子も似ているが、
量子の方にはmS=0がある
mS=0は実は赤道面内回転(揺らぎ最大)
J<0(Antiferromagnetic)・・・古典と量子はまるで違う
一重項=VB:
スピン量子揺らぎを最大限使って
外部にはいっさい磁気モーメントを見せない
1-1-5. 例題
(1)
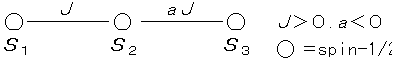
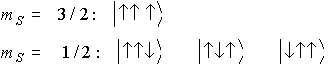
- 負のmSは、全部のスピンを同時に反転させれば正のmSと同等
- 異なるmSは別の行列
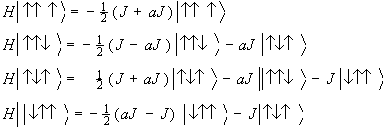
行列の作り方の公式:
- 対角項 :↑↑,↓↓に対して−J/2
↑↓,↓↑に対して+J/2
- 非対角項:↑↓と↓↑の交換で互いに移れる状態間に−J
mS=3/2・・・固有値0
mS=1/2・・・ 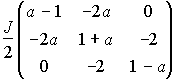 の対角化から
の対角化から
固有値
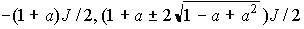
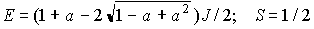 :基底状態(どんな?)
:基底状態(どんな?)
 :(mS=3/2を含むから)
:(mS=3/2を含むから)
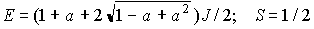
(2)
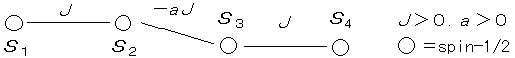
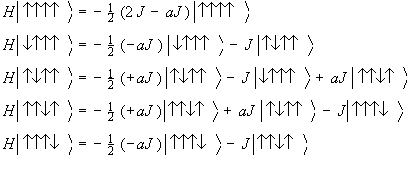
mS=2 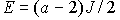 S=2
S=2
mS=1 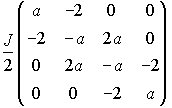 の対角化から
の対角化から
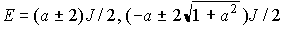
mS=0
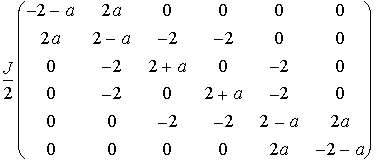 から
から
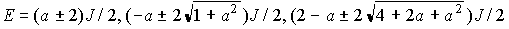
基底状態 :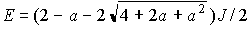 (S=0)
(S=0)
第1励起状態: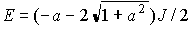 (S=1) との差は
(S=1) との差は
a
を大きくしても頭打ち(端のある量子反強磁性系の特徴)
(3)
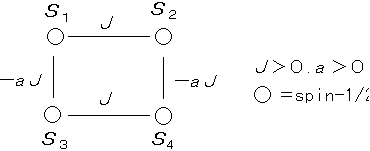
mS=2
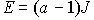 (S=2)
(S=2)
mS=1
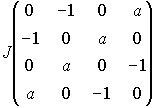 の対角化から
の対角化から
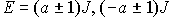 (S=2,1)
(S=2,1)
mS=0
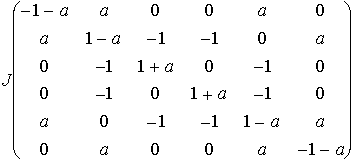 から
から
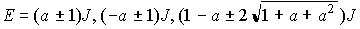
基底状態:
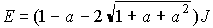 (S=0)
(S=0)
非常に安定・・・“二重結合”
(1−2) 補足的事項(観測される磁性に影響する要因)
1-2-1. スピン次元と空間次元
鎖:一次元、層:二次元
ただし、
- J の次元性の磁性への効き方
- t の次元性(バンドの異方性)の伝導性への効き方
は微妙に違う
「
異 方 性 は 磁化率・磁気共鳴から簡単に わ か る
が、
次 元 性 は なかなか わ か ら な い」
量子スピン系の本筋からはややズレるが・・・
異方性の原因(磁気共鳴では大事)
- 純粋な電子スピンは分子や結晶がどっちを向いているか知らない
- 周りの電子スピン&軌道角運動量に教えられる
- スピン-スピン双極子相互作用
- スピン-軌道相互作用
スピン-スピン双極子相互作用
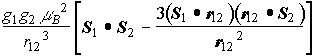
- 異方的な弱い交換相互作用に見える〜
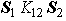
- 角度依存性:1-3 cos2θ
- 分子間で、スピンがオーダーしたときの磁気構造を決める
(磁化容易軸/困難軸)
- 不対電子2個以上の分子内の異方性
(single ion anisotropy = local anisotropy)
スピン-軌道相互作用
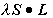 普通はg やJ に繰込まれる
普通はg やJ に繰込まれる
- --> g の異方性 => 磁化率の異方性(∝g
2)
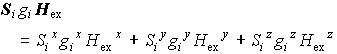
- --> J の異方性( ∝ (Δg /g
)2 )
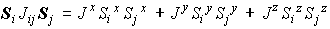
Stotalzが保存しなくなる
- --> Dzyaloshinsky-Moriya相互作用 (∝Δg /g
)
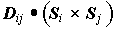
スピンどうし垂直になろうとする
対称性による制限
他に実験上重要な異方性として、反磁場効果(試料の外形に依存)
1-2-2.磁性体の熱力学
- 系のHamiltonian (エネルギー固有値)
−−> 分配関数 Z (H,T )
(Boltmann因子:exp(-E/kT) の和)
系が独立なN個の unitから成るとき、
系の分配関数=unitの分配関数のN乗
- 分配関数 −−> 自由エネルギー F=−kT
lnZ
- 自由エネルギー −−> 磁化M,エントロピーS
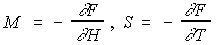
- 磁化 −−> 磁化率χ,エントロピー −−> 比熱C
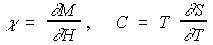
ついでに単位系...
cgsでは、
- 自由エネルギー:erg=g cm2 / s2
- 磁場:Oe (=G) ,磁束密度:G
- 磁化:erg / Oe (通称emu)
- 体積あたり磁化率:無次元(通称emu)
磁化率:
erg/Oe2=cm3(通称emu)
だから Oe2=erg/cm3
- モルあたり磁化率: cm3/mol(通称emu/mol)
反磁性・Pauli 常磁性 〜104
- Curie定数: cm3K/mol(通称emuK/mol)
独立な電子スピンのCurie定数0.375
磁性の研究現場でよく使われるが、通称が紛らわしく、
電磁誘導が絡むと厄介
SIでは、
- 自由エネルギー:J
- 磁場:A/m (あまり使わない?)
- 磁束密度:T(=10000G)
- 磁束:Wb=Tm2=Vs
- 磁化: A/m=Wbm/H
- インダクタンス:H=Wb/A
- 透磁率・磁化率:H/m
1-2-3.平均場近似
−−> Curie-Weiss則(磁性体の状態方程式)
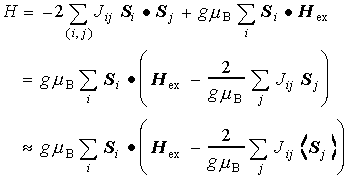
- Si =
<Sj> として、self-consistentに解く
- [ ] 内第2項を平均場(交換磁場)という
- 常磁性状態(Sjがランダムに配向)では、等方的!
- Hexがゼロなのに<Sj>がゼロでなくなるとき、
- 磁気秩序が生じている
- <Sj>が全部同符号
・・・ 強磁性の自発磁化
- <Sj>がj
によって符号をかえる・・・反強磁性の副格子磁化
(Staggered Magnetization)
Curie-Weiss則
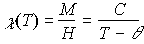
- C:スピンの数,
- θ∝ 交換相互作用×最近接スピンの数
高温・弱磁場(gμBH/kBT≪1)ではとにかく正しい
- 強磁場 −−>
飽和(Brillouin関数:Sが大きいほど早く飽和)
- 低温 −−> 揺らぎ(短距離秩序)/磁気秩序
1-2-4. マクロ系の基底状態いろいろ
- 磁気秩序 =縮重した状態から1つが選ばれる(対称性の破れ)
強磁性・反強磁性・フェリ磁性・スパイラル磁性...
- 乱れた状態=縮重した状態がそのまま凍結
(エントロピーがゼロにならない) Frustration
- 非磁性状態=唯一の基底状態(量子singlet)
磁気モーメントなし、秩序もなし
- 変わり種秩序:・Kosteritz-Thoules (KT)渦
磁気秩序に伴う物性の変化
- 磁化率の発散と非線型性
- 自発磁化や顕著な異方性の発生
- 秩序形成時に交換相互作用の役割はほとんど終わる
秩序化したスピンが向く方向は、残りの異方的相互作用で決まる
- 比熱に尖ったピークが出る(二次相転移)
- 磁気共鳴における緩和時間の異常
1-2-5.スピン波近似
- 基底状態が磁気秩序状態であるとき有効
- Curie-Weissより一歩前進
- 基底状態から波数qでスピンをわずかにねじった状態をつくったときの
励起エネルギーを計算
- Phononの分散やバンド計算に似たものが出る
- 強磁性の場合、 E ∝ cos(q )
- 反強磁性の場合、E ∝|q|
- Phononに対応させて、magnonという
- これを使って
- スピンが集団で運動することによる基底状態の補正
(スピン波間の相互作用で量子効果も入れる)
- 物性の計算
1-2-6.非磁性量子状態の簡単な例=電子スピンの二量化
高校化学の例(気相平衡反応)
2NO2 (褐色)-->
N2O4(無色)
- とにかく一番起こりやすいことの1つ
- 要するにVB(結合)ができること(原子内=内殻、分子内、分子間で)
- 3電子以上で1本のVBをつくることはない
- 1電子が正味2本のVBに参加することもない
- 典型的な量子効果
- スピンの向きは“なし”になる(秩序化すべきものがない)
- 量子的には明確な唯一の基底状態
- CDW
・・・・・・新しい単位格子内で2個の元伝導電子が非磁性化
(バンド絶縁体)
- Spin
Peierls・・・新しい単位格子内で2個の局在電子が非磁性化
これら2つは格子歪み(単位格子の変更)を伴う
S-T(singlet-triplet)モデル=最初にやった2電子問題
- 格子歪みなし
- 局在2電子間にJ<0(反強磁性的)
- エネルギーギャップ=2J
(下に非磁性singlet、上にtriplet)
描像:
- kT>>Jではgapが無視できる --> 常磁性
- kT<<Jではtripletが無視できる--> 非磁性
- 磁化率はgapを越えて励起されたtripletの数で決まる
- 活性化型:低温で指数関数的に減少
- Curie“定数”が温度変化する
ここでは正統的計算で磁化率と比熱を求める
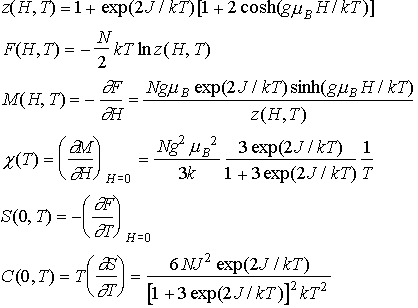
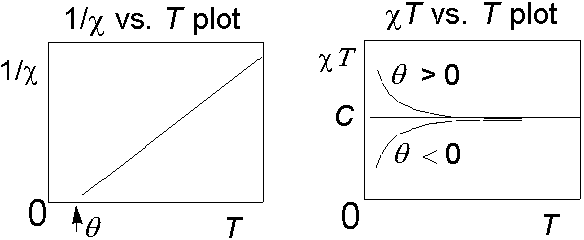
- χやC
はどんな温度変化?(Schottky比熱)その意味は?
- χの極大で、
- Tmax=1.25|J|/k,
- χmax=0.15094k/|J|
- T=0で、M の磁場依存性は?
Crossover ・・・ 相転移ではない
- 一次相転移:自由エネルギーの交差
- 二次相転移:対称性の破れ
1-2-7.量子効果 vs.
磁気秩序・・・どっちになるか?(次元性の役割)
磁気秩序を有利にする条件:異方性(量子性の破壊) &
高次元(最近接スピン数)
次元性の役割(J <0の場合):
- 相手1個と量子singlet(VB)をつくって J の得
- 相手z個と反対向いて(Neel状態) 〜 zJ
s・s´ = zJ /4の得
概ね二次元 ( z =3-6 ) あたりが境目
実際に長距離秩序が実現するかどうかは微妙な問題
(Mermin-Wagner, Kosteritz-Thouless, ...)
スピンの揺らぎ ・・・ この言葉、いろんな意味で使われている
- スピンの量子揺らぎ:まっすぐ磁場方向を向かず、歳差運動(零点振動)していること
- スピンの横揺らぎ
:スピンの方向の自由度があること
- スピンの縦揺らぎ
:スピンの大きさの自由度があること
量子singletの中では、量子揺らぎが最大
対全体としては横揺らぎも縦揺らぎもゼロ
- 注意 :
非磁性singlet状態を“乱れた状態”と呼ぶことがある
- 注意 :
磁気秩序のない量子状態をスピン液体と総称するらしい
〒274 船橋市三山2-2-1 東邦大学 理学部 物理学科
Phone : 0474-72-6988, F A X : 0474-75-1855
田村 雅史
tamura@ph.sci.toho-u.ac.jp
:交換相互作用 exchange coupling
演算子を成分とするベクトル
:Bohr磁子magneton
:g テンソル(3×3行列)
:外部磁場
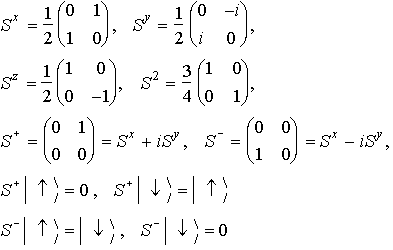
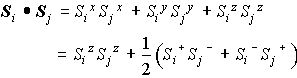
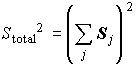 も変えない
も変えない
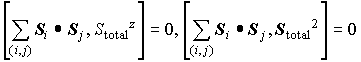
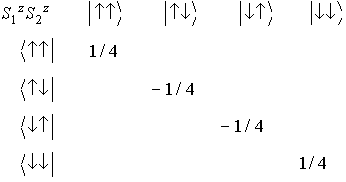

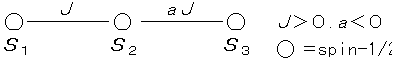
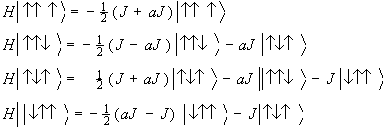
の対角化から
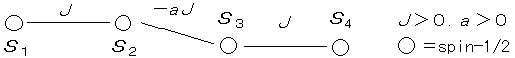
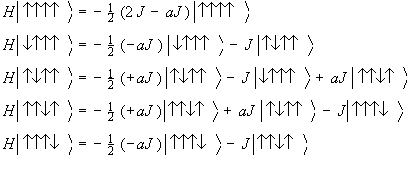
S=2
の対角化から
から
(S=0)
(S=1) との差は
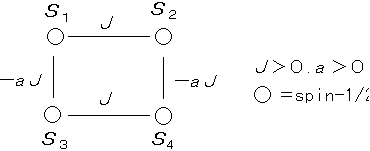
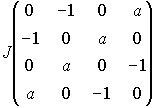 の対角化から
の対角化から(S=2,1)
から
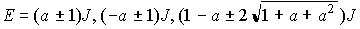
(S=0)